SHI Weixiu
,
JI Xueyuan
,
PAN Lisheng
,
SUN Yin
,
LI Chaoqi
,
WEI Xiaolin
. Centrifugal Pressurization Process in the Near Critical Region for Supercritical CO2 Brayton Cycle[J]. 热科学学报, 2025
, 34(5)
: 1912
-1924
.
DOI: 10.1007/s11630-025-2188-0
The starting point for the pressurization process of a supercritical CO2 Brayton cycle is near the critical point, which may lead to a liquid hammer if the inlet pressure fluctuates. It is important to judge whether the phase change of working fluid occurs during the pressurization process. With CO2 as the working fluid, the pressurization process for a centrifugal pressurization component is attention considered and analyzed. Specifying the inlet temperature, inlet pressure and outlet pressure as 32°C, 7.4 MPa and 24 MPa, respectively, the thermodynamic parameters of key state points of a centrifugal pressurization component are obtained. At the entrance of the impeller, a phase change of CO2 may occur, especially when the inlet points are close to the critical point. A method using enthalpy difference and exergy difference to express the possibility CO2 phase change is proposed. Furthermore, the risk degree of CO2 phase change is represented visibly. In view of the power consumption and efficiency of compressors under different working conditions, the changes of power consumption, isentropic efficiency and internal efficiency of compression components were analyzed under the conditions of constant outlet pressure and constant pressurization ratio. The power consumption is affected by the specific volume of the working fluid and the pressure difference. With the same inlet conditions, the isentropic efficiency under constant pressurization ratio is higher than that under a constant outlet pressure due to the lower power consumption; the internal efficiency is higher than the isentropic efficiency, and the trend is similar. This method can contribute to the setting of safe conditions for pressurization components.
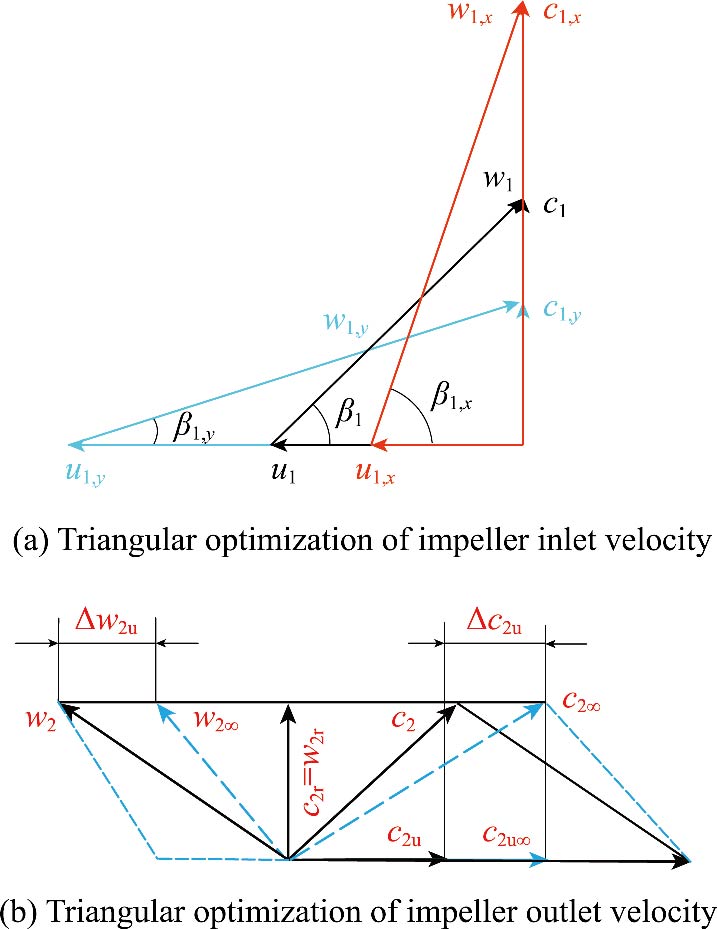
[1] National Development and Reform Commission. Action Plan for Energy Technology Revolution and Innovation, 2016.
[2] World Energy Outlook 2020, International Energy Agency.
[3] National Energy Administration, Outline of the 13th Five-Year Plan for National Economic and Social Development of the People’s Republic of China, 2016.
[4] Liu Y., Wang Y., Huang D., Supercritical CO2 Brayton cycle: A state-of-the-art review. Energy, 2019, 189: 115900.
[5] Ahn Y., Bae S.J., Kim M., et al., Review of supercritical CO2 power cycle technology and current status of research and development. Nuclear Engineering and Technology, 2015, 47(6): 647–661.
[6] Pan L., Li B., Wei X., et al., Experimental investigation on the CO2 transcritical power cycle. Energy, 2016, 95: 247–254.
[7] Guelpa E., Verda V., Exergoeconomic analysis for the design improvement of supercritical CO2 cycle in concentrated solar plant. Energy, 2020, 206: 118024.
[8] Ochoa G.V., Forero J.D., Rojas J.P., A comparative energy and exergy optimization of a supercritical-CO2 Brayton cycle and Organic Rankine Cycle combined system using swarm intelligence algorithms. Heliyon, 2020, 6(6): 2405–8440.
[9] Li H., Zhang Y., Yao M., et al., Design assessment of a 5 MW fossil-fired supercritical CO2 power cycle pilot loop. Energy, 2019, 174: 792–804.
[10] Ding H., Zhang Y., Hong G., et al., Comparative study of the supercritical carbon-dioxide recompression Brayton cycle with different control strategies. Progress in Nuclear Energy, 2021, 137: 103770.
[11] Baltadjiev N.D., Lettieri C., Spakovszky Z.S., An investigation of real gas effects in supercritical CO2 centrifugal compressors. Journal of Turbomachinery, 2015, 137(9): 091003.
[12] Zheng K., Zhao H., Feng Z., Analysis of internal flow characteristics in a supercritical CO2 centrifugal compressor. Journal of Engineering Thermophysics, 2015, 36(5): 985–988.
[13] Xu P., Zou Z., Fu C., Aerodynamic design considerations for supercritical CO2 centrifugal compressor with real-gas effects. Energy Conversion and Management, 2022, 271: 116318.
[14] Shao W., Yang J., Wang X., et al., Accuracy study and stability control of a property-table-based CFD strategy for modeling SCO2 compressors working near the critical point of the fluid. Applied Thermal Engineering, 2021, 183(2): 116222.
[15] Pan L., Wei X., Shi W., Theoretical investigation on a novel CO2 transcritical power cycle. Journal of Engineering Thermophysics, 2015, 36(6): 1182–1185.
[16] Pan L., Li B., Shi W., et al., Optimization of the self-condensing CO2 transcritical power cycle using solar thermal energy. Applied Energy, 2019, 253: 113608.
[17] Pan L., Shi W., Wei X., et al., Experimental verification of the self-condensing CO2 transcritical power cycle. Energy, 2020, 198: 117335.
[18] Pan L., Wei X., Shi W., Performance analysis of a zeotropic mixture (R290/CO2) for trans-critical power cycle. Chinese Journal of Chemical Engineering, 2015, 23(3): 572–577.
[19] Pan L., Ma Y., Li T., et al., Investigation on the cycle performance and the combustion characteristic of two CO2-based binary mixtures for the transcritical power cycle. Energy, 2019, 179: 454–463.
[20] Shi W., Pan L., Jin S., et al., Combustion characteristic and mechanism of a mixture working fluid C3H8/CO2. Journal of Thermal Science, 2021, 30(05): 1768–1779.
[21] Zhu M., Principle of turbocharger. Beijing: National Defense Industry Press, 1982.
[22] Lemmon E.W., Huber M.L., McLinden M.O., NIST Standard Reference Database 23, Reference Fluid Thermodynamic and Transport Properties (REFPROP), version 9.0, National Institute of Standards and Technology, 2010.



